Introduction to Image Restoration Methods – Part 1

This is the first part of a small series of articles on various image restoration methods used in digital image processing applications. We will try to present the bird’s-eye perspective of concepts of different restoration techniques but not to dive too deep into the math and theoretical intricacies, although we assume that the reader has some understanding of discrete mathematics and signal processing basics.
Basic Concepts
The goal of the image restoration is to recover an image that has been blurred in some way. In computational image processing blurring is usually modeled by a convolution of image matrix and a blur kernel. A blur kernel in this case is a two-dimensional matrix which describes the response of an imaging system to a point light source or a point object. Another term for it is Point Spread Function (PSF).
What does it mean?
Let’s suppose we have three two-dimensional matrices: f(x,y) for the original image, h(m,n) for the blurring kernel and g(x,y) for the blurred image. Than we can write the convolution: 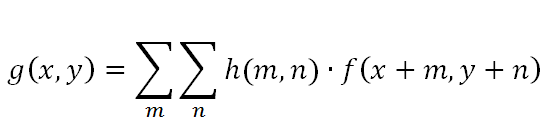
or, using asterisk to denote convolution operation,
g = f * h.
The above equation is written in spatial domain because we use spatial coordinates (x,y), but the convolution result can be described in a more convenient way in frequency domain using frequency coordinates (u,w). From the convolution theorem the Discrete Fourier Transforming (DFT) of the blurred image is the point-wise product of the DFT of the original image and the DFT of the blurring kernel:
G(u,w) = F(u,w) * H(u,w)
where:
F(u,w) = DFT{f (x,y)},
G(u,w) = DFT{g(x,y)} and
H(u,w) = DFT{h (x,y)} for blurring kernel.
The most common types of blur are motion blur, out-of-focus blur and Gaussian blur (it’s a good approximation of an image degrading by atmospheric turbulences).
There are several widely used techniques in image restoration, some of which are based on frequency domain concepts while others attempt to model the degradation and apply the inverse process. The modeling approach requires determining the criterion of “goodness” that will yield an “optimal” solution.
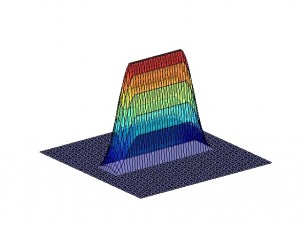
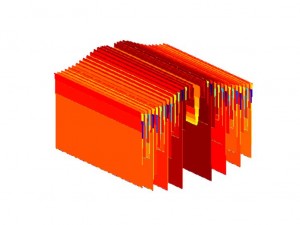
Picture 1: Motion blur kernel
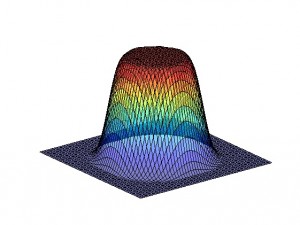
Picture 2: Out-of-focus blur kernel
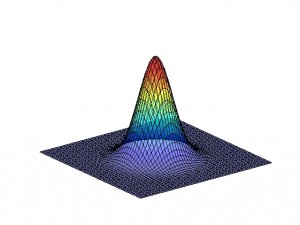
Picture 3: Gaussian blur kernel
In this article, we will demonstrate the simplest methods of image restoration when the actual spatial convolution filter (i.e., the type of the blur) used to degrade an image is known. It is important to understand that all the examples were artificially created (using motion blur kernel) to show the basic concept of image restoration techniques.

Picture 4: Original image Lenna

Picture 5: Degraded image (motion blur is applied here)
Inverse Filtering
The idea of the inverse filtering method is to recover the original image from the blurred image by inversing blurring filter. We assume that no additional noise is present in the system.
We need to find such a filter kernel r(x,y) that its convolution with the blurred image could produce a result close to the original image:
g * r = f,
(f * h) * r = f
or since the convolution operation is associative and has a multiplicative identity,
h * r = Оґ,
where Оґ(x,y) is the Kronecker’s delta function.
Then, applying the convolution theorem in the frequency domain we obtain:
H(u,w) * R(u,w) = 1.
Thus, dividing the DFT of the blurred image by the DFT of the kernel, we can recover (in theory) the original image. Then the inverse filter in frequency domain is simply R(u,w) = Rinv(u,w) in frequency domain is 1 / H(u,w).
Using point-wise multiplication of inverse filter Rinv(u,w) with Fourier transform of the blurred image G (u,w), we get Fourier transform of the restored image. Now using inverse DFT we obtain the final restored image.
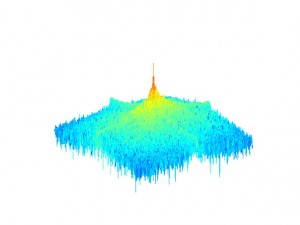
Picture 6: Spectrum of the original image
Picture 7: Spectrum of the motion blur kernel
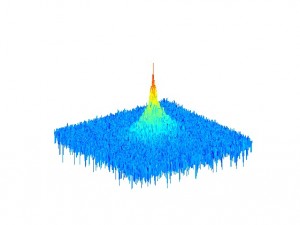
Picture 8: Spectrum of the degraded (blurred) image

Picture 9: Spectrum of the inverse filter
Wiener Filtering
The second technique widely used in image restoration is known as a Wiener filtering. This restoration method assumes that noise which is present in the system is additive white Gaussian noise and it minimizes mean square error between original and restored images. Wiener filtering normally requires prior knowledge of the power spectra (spectral power densities) of the noise and the original image. Spectral power density is a function that describes power distribution over the different frequencies.
A simplified equation of the Wiener filter Rw is given below:
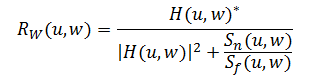
where Sn(u,w) is the spectral power density of the noise and Sf(u,w) is the spectral power density of the image.
Then using inverse DFT we obtain the restored image.
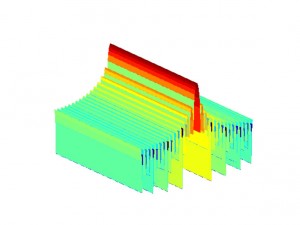
Picture 10: Spectrum of the Wiener filter
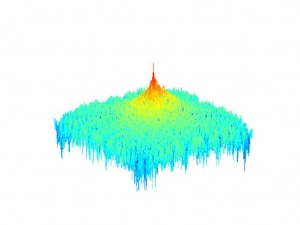
Picture 11: Spectrum of the Wiener-filtered image
Often, we can assume that
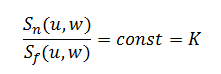 The inverse filter of a blurred image is a high pass filter. The parameter K of the Wiener filter is related to the low frequency aspect of the Wiener filter. The Wiener filter behaves as a band pass filter, where the high pass filter is an inverse filter and the low pass filter is specified by the parameter K. Note how Wiener filter becomes an inverse filter when K = 0.
The inverse filter of a blurred image is a high pass filter. The parameter K of the Wiener filter is related to the low frequency aspect of the Wiener filter. The Wiener filter behaves as a band pass filter, where the high pass filter is an inverse filter and the low pass filter is specified by the parameter K. Note how Wiener filter becomes an inverse filter when K = 0.
Below you can see the comparison of restoration results obtained by using inverse filter and Wiener filter.

Picture 12: Image restored with inverse filter

Picture 13: Image restored with Wiener filter
Conclusion
We can describe the image blurring process in most common cases as its convolution with some blur kernels. To restore degraded image we use deconvolution techniques such as inverse filtering and Wiener filtering. But we can observe that even in our examples (where the image was first artificially blurred by convolution) we didn’t get the expected results — restored images do not look exactly like the originals (especially for inverse filtering). This happens because small values of the Fourier transformed blur kernel turn to big ones of the restoration filter which significantly amplifies the noise.
What do we do to reduce noise level?
In real-life applications, we use another set of image restoration techniques — much more sophisticated iterative restoration methods. We will discuss these methods in the second part of this small series.
References
Wiener N (1964). Extrapolation, Interpolation, and Smoothing of Stationary Time Series. Cambridge, Mass: MIT Press. ISBN 0-262-73005-7.