Introduction to Image Restoration Methods – Part 2 Iterative Algorithms
This is the second part of a small series of articles on various image restoration methods used in digital image processing applications, in which we try to present the bird’s-eye perspective of some concepts of different restoration techniques without diving too deep into the math and theoretical intricacies. We assume that the reader has some understanding of discrete mathematics and signal processing basics.
Click here to read the first part.
Iterative algorithms
The simplest iterative algorithm for image restoration was first described by Van Cittert in 1930. The equation of this algorithm can be written as
f n+1 = f n + (g — h* f n),
where f n+1 is the new estimate of the image matrix derived from the previous one — f n,В f 0 = g is the blurred image, n is the number of the current step of the iteration, f is the blur kernel (point spread function, or PSF), and * sign denotes a convolution operator.
The Van Cittert algorithm (see more in German wiki) has many advantages, such as rapid deblurring, contains only a few variables and rather simple mathematical operations, and does not require smoothness restrictions or additional information. On the other hand, it has some major limitations. For example, the algorithm is sensitive to the presence of noise, and it increases the noise amounts in the deblurred image tremendously. Also, it becomes unstable if the number of iterations exceeds a certain limit, and the resultant image starts to look shaky.
The Landweber iteration, or Landweber algorithm, is an algorithm most frequently used to solve ill-posed linear inverse problems, although it has been extended to solve non-linear problems that involve constraints as well. The method was first proposed in the 1950s. It is now considered to be a base for many other iterative image restoration methods.
The equation of the Landweber algorithm is (using the same notation as for the previous formula):
f n+1 = f n + ОІhT В (g — h * f n),
where constant ОІ controls and regularizes the sharpening effect of the algorithm, and hT denotes a transposed matrix h.
The Landweber algorithm is an enhanced version of the Van Cittert algorithm. The introduction of the termВ ОІhT results in an algorithm that is more stable in the presence of noise and more reliable when performing an additional number of iterations, resulting in a less shaky image.
The Richardson—Lucy algorithm, also known as Lucy—Richardson deconvolution, is an iterative procedure for recovering a latent image that has been blurred by a known point spread function.
The equation of the Richardson-Lucy algorithm is as follows: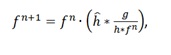 where the division and multiplication are performed element-wise, and ДҐ is the flipped point spread function.
where the division and multiplication are performed element-wise, and ДҐ is the flipped point spread function.
The Richardson-Lucy algorithm is one of the most popular deblurring algorithms in the area of image processing due to many reasons. For example, although developed specifically for restoration of astronomical images where the noise is mainly Poisson-distributed, it performs sufficiently well with any type of noise in the image. В This algorithm also does not require any information from the original (latent) image. The Richardson-Lucy algorithm remains applicable in the event of the noise present, but the level of the noise increases with the increase of the number of iterations.
The Poisson MAP (Maximum a posteriori estimation) algorithm is another interesting iterative algorithm. Its variables are the same as in the Richardson-Lucy algorithm, the only difference between the two algorithms is that the Poisson MAP uses the exponential operation in the restoration process. The equation of the Poisson MAP algorithm, thus, is: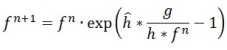 This approach has some advantages: introduction of the exponent assures pixel value non-negativity (which prevents processing artefacts) and non-linearity allows superresolution, i.e. recovery of spatial frequencies above the diffraction limit.
This approach has some advantages: introduction of the exponent assures pixel value non-negativity (which prevents processing artefacts) and non-linearity allows superresolution, i.e. recovery of spatial frequencies above the diffraction limit.
And now let us demonstrate how these methods work in practice.
Here is an original image used for demonstration. It’s a photo of a computer monitor obtained with a cell phone. This image contains a complex type of blurring, including both out-of-focus and motion, blurs, which makes it a difficult and interesting object for restoration.
We can use MATLAB’s deconvlucy function to deblur the image using the accelerated, damped Lucy-Richardson algorithm. The algorithm maximizes the likelihood of the resulting image, when convolved with the PSF, being an instance of the blurred image, assuming Poisson noise statistics. This function can be effective when you know the PSF, but know little about the additive noise present in the image.
The deconvlucy function implements several adaptations to the original Lucy-Richardson maximum likelihood algorithm that address complex image restoration tasks.
Picture 1: Original image
Picture 2: Image restored with Richardson-Lucy deconvolution
One way of reducing artifacts is through the use of a prior knowledge of the original image. If the image data, for example, consists of blurred bright points on black background (astronomical imaging or photographed text), the ringing contains negative intensity values. Introducing a positivity constraint during the restoration can prevent this ringing. The iterative restoration procedures that were presented above are particularly effective for ringing reduction when the constraints can be made tight.
Picture 3: Image restored with Richardson-Lucy deconvolution with positivity constraint
To obtain results of even higher quality we can combine different deconvolution algorithms. Picture below shows the result of this approach.
Picture 4: Image restored with an improved algorithm
Applying iterative methods, which incorporate some constraints at each iteration, usually produces much better results of image restoration than using Wiener filtering. The disadvantage of iterative methods is that they may take quite a lot of processing time.
Yet, all the image restoration methods cannot improve image resolution. Special image processing techniques known as superresolution are used for this. We will discuss these techniques in one the next parts of the series.
References
- Biemond, J.; Lagendijk, R.L.; Mersereau, R.M. Iterative methods for image deblurring.В Proceedings of the IEEEВ , vol.78, no.5, pp.856,883, May 1990. doi: 10.1109/5.53403
- Landweber, L. An iteration formula for Fredholm integral equations of the п¬Ѓrst kind. Amer. J. Math. 73, 615—624
- Richardson, William Hadley Bayesian-Based Iterative Method of Image Restoration.В JOSAВ 62В (1): 55—59.В doi:10.1364/JOSA.62.000055.
- Lucy, L. B. An iterative technique for the rectification of observed distributions. Astronomical JournalВ 79В (6): 745—754.В Bibcode:1974AJ…..79..745L.В doi:10.1086/111605.